
The greatest possible fall in energy will therefore produce the highest frequency line in the spectrum. The last equation can therefore be rewritten as a measure of the energy gap between two electron levels: That energy must be exactly the same as the energy gap between the 3-level and the 2-level in the hydrogen atom. From the frequency of the red light, its energy can be calculated. This is the origin of the red line in the hydrogen spectrum. If an electron falls from the 3-level to the 2-level, red light is seen. The higher the frequency, the higher the energy of the light. Each frequency of light is associated with a particular energy by the equation: That energy which the electron loses is emitted as light (which "light" includes UV and IR as well as visible radiation). If an electron falls from the 3-level to the 2-level, it must lose an amount of energy exactly equal to the energy difference between those two levels. It could fall all the way back down to the first level again, or it could fall back to the second level and then, in a second jump, down to the first level.Īssigning particular electron jumps to individual lines in the spectrum It would tend to lose energy again by falling back down to a lower level. Suppose a particular electron is excited into the third energy level. Hydrogen molecules are first broken up into hydrogen atoms (hence the atomic hydrogen emission spectrum) and electrons are then promoted into higher energy levels. The high voltage in a discharge tube provides that energy. But if energy is supplied to the atom, the electron is excited into a higher energy level, or even removed from the atom altogether. When unexcited, hydrogen's electron is in the first energy level-the level closest to the nucleus. Why does hydrogen emit light when excited by a high voltage and what is the significance of those whole numbers? Each line can be calculated from a combination of simple whole numbers. The lines in the hydrogen emission spectrum form regular patterns and can be represented by a (relatively) simple equation. The origin of the hydrogen emission spectrum The various combinations of numbers that can be substituted into this formula allow the calculation the wavelength of any of the lines in the hydrogen emission spectrum there is close agreement between the wavelengths generated by this formula and those observed in a real spectrum.Ī modified version of the Rydberg equation can be used to calculate the frequency of each of the lines: In other words, if \(n_1\) is, say, 2 then \(n_2\) can be any whole number between 3 and infinity. \(n_1\) and \(n_2\) are integers (whole numbers).
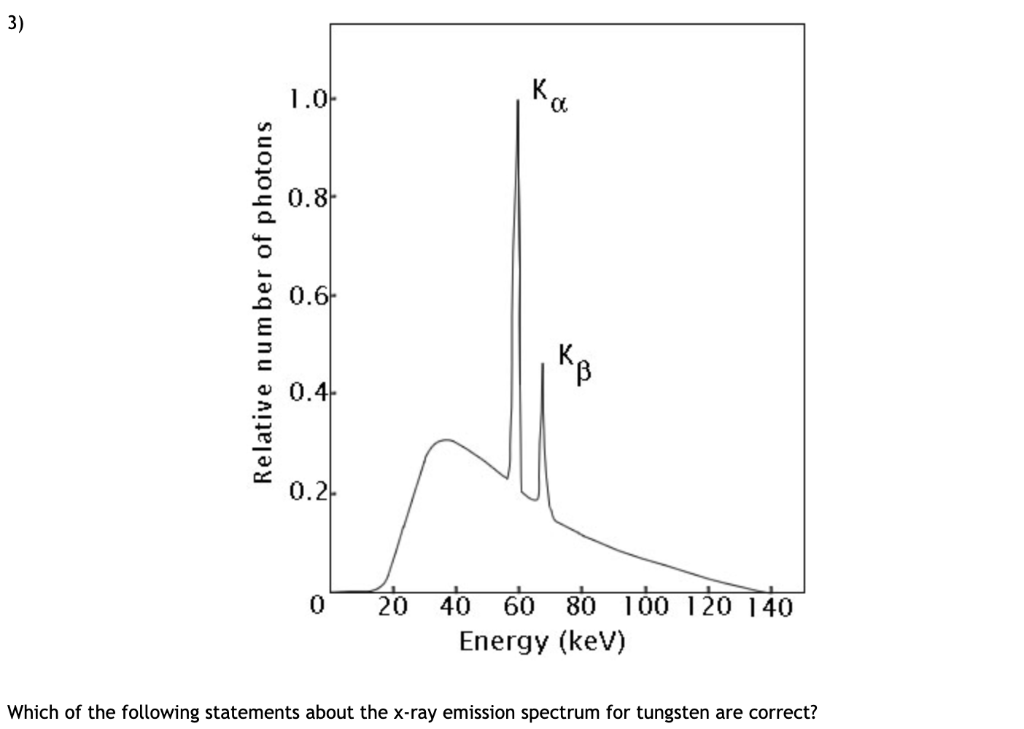
Hydrogen molecules are first broken up into hydrogen atoms (hence the atomic hydrogen emission spectrum) and electrons are then promoted into higher energy levels.\right)\]



 0 kommentar(er)
0 kommentar(er)
